Метод сил
Общая идея метода сил, применительно к контактным задачам
Прежде чем рассматривать метод сил применительно к контактным задачам, введем несколько понятий и допущений:
1)для простоты изложения будем рассматривать контакт только 2-х тел. Идею используемого метода можно легко развить для расчета контакта произвольного количества тел, а также на случай контакта в пределах одного тела;
2)для простоты изложения будем рассматривать контакт на плоскости. Идея метода легко обобщается на пространственный случай;
3)чисто условно обозначим одно тело активным, а другое - пассивным. Узлы активного тела будем называть активными, а пассивного - пассивными;
4)пара контакта – 2 узла конечно-элементной сетки, находящиеся напротив друг друга на активной и пассивной поверхностях.
Метод сил – это метод определения неизвестных усилий в связях исходной системы. Согласно методу вместо исходной системы вводится т.н. основная система, в которой действуют те же внешние силы, что и в исходной системе. Помимо этого из основной системы исключаются связи с реакциями, которые подлежат определению. Эти связи заменяются неизвестными силами, направление которых совпадает с направлением этих связей. Значения этих сил и будут искомыми неизвестными переменным канонической системы уравнений метода сил. Каждое такое уравнение говорит об отсутствии перемещения в точке с разрушенной связью, для которой составляется конкретное уравнение, в направлении этой же связи. При этом для составления системы уравнений необходимо знать значения перемещений во всех точках с отброшенными связями от действия в каждой из этих точек единичной силы, а также от действия внешней нагрузки.
Система канонических уравнений метода сил, имеет вид:
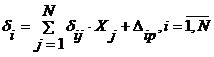(3.1)
где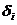
- величина перемещения i -той точки в направлении действия силы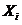 
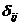- коэффициенты влияния, т.е. перемещения в i-той точке в направлении действия силы 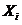от действия приложенной в j-той точке единичной силы;
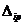- перемещение в i-той точке в направлении действия силы 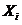от действия внешней нагрузки.
Рассмотрим теперь подробно этот метод сил применительно к контактной задаче. Начнем рассмотрение метода с выяснения, что собой представляет исходная система. Исходная система согласно изложенным выше положениям метода сил представляет собой систему с ограничениями, в которых действуют неизвестные реакции. Применительно к контактной задачи этими ограничениями для каждого из тел будут являться поверхности другого тела, вошедшие в контакт, т.к. они запрещают дальнейшее перемещение точек рассматриваемого тела. После осмысления этого не особо сложного факта, становится ясно, что неизвестные контактные усилия в активных и пассивных узлах, вошедших в контакт, и являются теми самыми неизвестными реакциями в связях, наложенных на систему.
Итак, допустим, что из каких-либо соображений мы задались конкретными размерами пятна контакта, т.е. задали набор точек на активной и пассивной поверхностях, которые должны совпасть в результате сжатия и оказаться на общей плоскости контакта 2-х тел. На рис. 2.5 представлена такая условная исходная система, для которой необходимо определить значения контактных усилий в этих узлах [3].
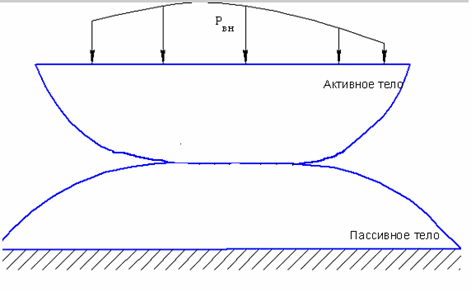
Рис. 3.1. Исходная схема
Следующим важным понятием метода сил является основная система. Она вводится, как исходная система, в которой ограничения, наложенные на интересующие нас точки, заменены неизвестными реакциями. В качестве геометрии такой системы можно принять геометрию нашей конечно-элементной модели, в узах которой мы и будем прикладывать единичные силы. А именно в каждом из узлов пятна контакта, принятого для исходной системы, мы прикладываем силу Х, величину которой мы будем определять из решения канонической системы уравнений (рис. 3.2).
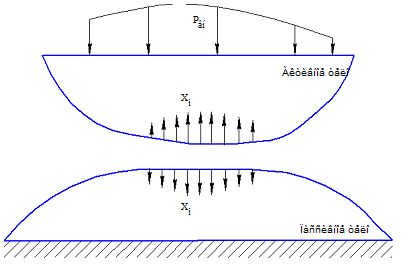
Рис. 3.2. Основная система
Важно, чтобы основная системы была кинематически неизменяема, иначе станет невозможным определение коэффициентов влияния (податливости) для контактных узлов активной и пассивной поверхностей. Поэтому, если тело не обладает набором связей, необходимых для обеспечения его полной неподвижности, нужно ввести эти дополнительные связи. Так, в нашем случае, надрессорная балка является полностью неподвижной и не нуждается в дополнительных связях, пятник же тело полностью свободен, поэтому необходимо наложить на него 6 дополнительных связей, которые будут запрещать его возможные перемещения.
Перейдем теперь собственно к составлению самой канонической системы уравнений. Для составления этой системы нам необходимо знать следующие параметры:
1)коэффициенты взаимного влияния от единичных сил приложенных в узлах предполагаемого контакта, представляющие собой перемещение каждого из узлов в направлении внутренней нормали в этом узле;
2)перемещение от внешней нагрузки в узлах предполагаемого контакта;
3)начальные зазоры между соответствующими узлами активной и пассивной поверхности.
Подводя итог всему вышесказанному, можно сказать, что каждое уравнение канонической системы метода сил применительно к контактной задаче, по сути, выражает собой величину зазора между соответствующими активными и пассивными узлами через силы, действующие в контакте, для каждой пары контакта. Поскольку точно сказать заранее, какие именно точки войдут в контакт, нельзя, то процесс нахождения точного решения будет последовательным.
