Основная система и уравнения равновесия
Анализируя все неизвестные переменные в задаче плоского контакта 2-х тел , легко заметить, что помимо неизвестных реакций связи неизвестными переменными также являются перемещения тел, как абсолютно твердых. Например, в рассматриваемой задаче (рис. 3.2) активное тело в процессе перехода в деформированное состояние может получить горизонтальное и вертикальное перемещения, а также повернуться на некоторый угол. Пассивное тело является жестко закрепленным, поэтому оно не вносит новых неизвестных. Таким образом, за счет кинематической подвижности активного тела, мы получаем 3 новые неизвестных величины. В то же время метод сил может дать нам лишь уравнения, достаточные для определения неизвестных, в количестве неизвестных контактных сил, что является явно недостаточным для определения неизвестных перемещений тел, имеющих ненулевые степени свободы. Такое противоречие легко устраняется, если помимо уравнений метода сил, отражающих деформационную сторону задачи, ввести в рассмотрение еще и уравнения равновесия, отражающие силовую сторону, которые также обязано должны выполняться. Как будет показано дальше, правильность составления уравнений равновесия некоторым образом связана с выбором основной системы.
Начнем с того, что введение основной системы, требует предварительного определение степеней свободы каждого из тел, как абсолютно твердого тела, хотя бы потому, что в основной системе каждое тело является кинематически неподвижным. Известно, что положение любого тела на плоскости (мы рассматриваем упрощенный плоский вариант), характеризуется 3-мя компонентами перемещений, связанными с каким-либо полюсом тела. Зная начальное положение этого полюса и компоненты перемещения тела, связанные с ним, можно определить конечные координаты любой точки этого тела на плоскости. В качестве полюса для каждого из тел удобно выбрать начало координат. Тогда новое положение произвольной точки с начальными координатами (x,y) будет определяться как:
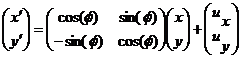(3.2)
где 
, 
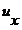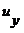и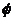 
- перемещения полюса и угол поворота около него.
Учитывая малость угловых перемещений в задачах контакта, выражение (3.2) можно упростить:
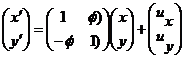(3.3)
Перейдем теперь к собственно анализу степеней свободы тела. Пусть на тело наложено M связей. Для каждой из них можно составить уравнение, означающее отсутствие перемещений в заданном направлении, которое легко получается из выражения (3.3). Например, выражение для горизонтальной связи, приложенной в точке с координатой (x,y) записывается как:
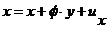(3.4)
Аналогично, записывается уравнение для вертикальной связи:
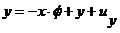(3.5)
Составив для всех связей, наложенных на тело, уравнения подобные уравнениям (3.4) и (3.5), получим однородную систему М уравнений относительно переменных 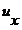, 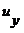и 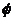. Очевидно, что матрица системы А может быть прямоугольной, поскольку количество связей может быть произвольным. Однако это не имеет принципиального значения для анализа степеней свободы тела. Полученную матрицу А можно упростить на основе несколько модифицированного метода исключения Гаусса, адаптированного к прямоугольному виду матрицы. В результате этого упрощения получим матрицу, которая может содержать строки следующего вида:
1) пустые строки, означающие бесполезность соответствующих связей с точки зрения подвижности тела, как абсолютно твердого тела;
2) строки, содержащие одно ненулевое число, означающие полное отсутствие соответствующего перемещения;
3) строки, в которых количество ненулевых элементов больше 1. Эти строки означают линейную связь между степенями свободы тела.
Совершив этот не особо сложный анализ кинематики тела, можно перейти к анализу наложенных на него связей. Для начала введем такое понятие, как необходимость связи. Необходимость связи определяется ее геометрическим уравнением (3.4 и 3.5) Данное уравнение линейно относительно степеней свободы тела и однородно. Поэтому, если все степени свободы, входящие в уравнение связи запрещены, то данная связь не нужна при расчете контакта. Это объяснятся тем, что реакция данной связи может войти только в уравнения равновесия для определения тех степеней свободы, которые входят в ее уравнение. А поскольку данные степени свободы запрещены, то эти уравнения равновесия составлять не надо. Соответственно, если в уравнении связи присутствует хотя бы одно ненулевая степень свободы, то ее необходимо учитывать при решении канонической системы метода сил, и при составлении уравнений равновесия. Впрочем, следует отметить, что необходимые связи в схемах встречаются не так часто, и как правило на практике соответствуют или сферическим шарнирам, или осям вращения (хотя можно придумать и другие случаи, но они вряд ли будут иметь практический интерес).
Таким образом, для получения корректной основной системы необходимо из первоначальной конечно-элементной схемы удалить все необходимые связи. Такая на первый взгляд противоречивость выражения «удалить все необходимые связи» лишь кажущаяся. Все дело заключается в том, что нужны то нам не сами связи, а их реакции, получающиеся после удаления самих связей. Поэтому согласно методу сил сами связи следует удалить. В дальнейшем условимся, что необходимым связям будут соответствовать неисключенные реакции.
После определения всех степеней свободы каждого из тел, легко определить, какие связи нужно дополнительно добавить в основную систему (помимо тех, что уже есть в исходной конечно-элементной схеме), чтобы запретить ненулевые степени свободы.
