Алгоритм решения контактной задачи
Алгоритм решения трехмерной контактной задачи принципиально не отличается от плоской. Тело, к которому приложены внешние нагрузки будем называть активным. Для узлов, лежащих на контактных поверхностях, перемещения определяются с использованием специальных зависимостей, позволяющих установить, вошли ли они в контакт или вышли из него, найти значения нормальной и касательной составляющих силы взаимодействия, ограничить касательную составляющую, если между узлами есть микропроскальзывание.
При разделении тел на конечные элементы узлы на противолежащих контактных поверхностях располагаются так, что один из них помещается на предполагаемом направлении перемещения другого. Предположим, что узлы на n-й прогонке перемещаются по прямой из положения на (n-1)-й прогонке. Пусть узлы в исходном состоянии до начала итерационного процесса занимают положения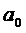 
, 
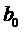, а на (n-1)-й прогонке положения 
, 
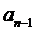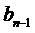и в контакт не входят. Выполняя блочную итерацию для каждого из узлов на n-й прогонке, с использованием уравнений (3.29) найдем приращения их перемещений 
, 
, 
, 
, 
, 
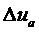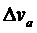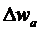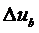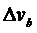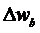в предположении, что они могут свободно перемещаться, не взаимодействуя с друг другом.
Для определения возможности внедрения узла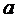 
в противолежащее тело при контактировании проведем через узел 
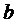плоскостью касательную к поверхности контакта. Если конечно-элементная сетка образована тетраэдрами, используем три узла, лежащие на пассивной поверхности в окрестности узла .
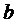Уравнение плоскости, проходящей через узлы 1-3
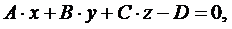(3.31)
где
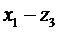- координаты узлов 1, 2, 3 с учетом их перемещений в местной системе, начало которой расположено в узле 1.
Умножив коэффициенты уравнения (3.31) на нормирующий множитель, получим направляющие косинусы нормали к касательной плоскости
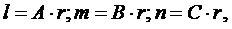(3.32)
где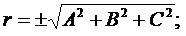 
знак r совпадает со знаком D.
Касательная плоскость, проходящая через узел 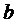, имеет те же направляющие косинусы нормали, а свободный член в ее уравнении
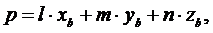
где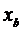 
, 
, 
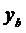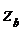- координаты узла 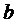, с учетом его смещения.
Нормальное уравнение касательной плоскости
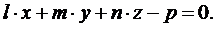(3.33)
Возьмем один из тетраэдров содержащий узел 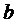, и найдем расстояние от его узла s, не лежащего на контактной поверхности, до касательной плоскости
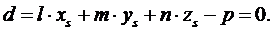
При использовании восьмиузловых конечных элементов касательная плоскость проводится параллельно хордам, соединяющим попарно по два соседних узла, лежащих на ортогональных координатных линиях. В этом случае удобно каждому контактному узлу приписывать четверку соседних узлов и узел, лежащий под контактной поверхностью.
Рассмотрим алгоритм определения условий взаимодействия двух сопряженных контактных узлов. С использованием уравнений (3.29) определяются приращения перемещений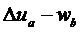 
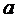узлов и 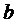в предположении, что они могут перемещаться свободно, не взаимодействуя друг с другом. При определении приращения перемещений каждого узла в уравнения вводятся соответствующие компоненты матрицы жесткост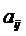и 
и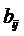 
. Текущие координаты узла 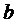с учетом его перемещений
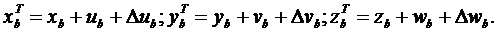(3.34)
Проведем через него касательную плоскость и найдем расстояние от узла 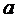до этой плоскости, подставив его координаты
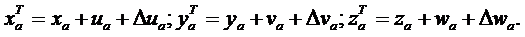(3.35)
в уравнение касательной плоскости (3.33)
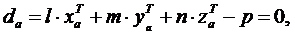
где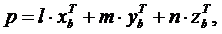 
Если знаки расстояни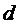й 
и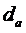 
не совпадают, то узла 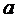и 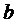не контактируют друг с другом и им приписываются вычисленные приращения перемещений 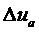- 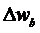. Если знаки не совпадают, узлы находятся в контакте и решение необходимо продолжить.
Проекции свободного перемещения узла 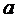на нормаль к касательной поверхности
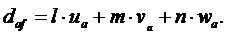(3.36)
На внедрение узла 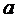в противолежащее тело приходится доля этого перемещения 
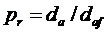, а на свободное перемещение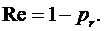 
Остановим узел 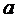в точке его встречи с касательной плоскостью, наложив на него связи. Силы, возникающие в этих связях, найдутся как правые части уравнений (3.29) при подстановке в их левые части компонентов матрицы жесткости области из конечных элементов, прилегающие к узлу 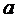, и невыбранных приращений перемещений
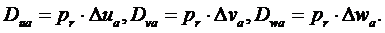(3.37)
вычисления совместного перемещения узлов 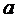и 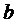вновь воспользуемся уравнениями (3.29), подставив в их правые части вычислены силы, а левую – суммарные компоненты матриц жесткости областей, прилегающих к узлам 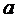и ,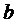
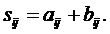(3.38)
Решение системы уравнений (3.29) дает значения компонентов совместного перемещения узлов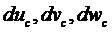 
. Невыбранные перемещения узла 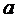теперь составляют 
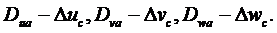Вводя их и компоненты матрицы жесткости области, прилегающей к узлу 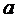, в системе уравнений (3.29), в правой части получим значения сил взаимодействия 
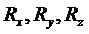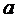узлов и 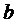.Нормальная и касательная составляющие силы взаимодействия контактирующих узлов найдутся через их проекции:
(3.39)
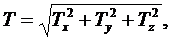
где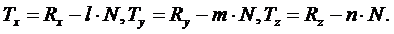 
В случае, если касательная сила не достигает ограничения по трению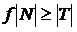 
, то узлы не проскальзывают относительно друг друга, на этом итерация для пары контактирующих узлов завершается и им приписываются перемещения
(3.40)
Если касательная сила больше силы трения скольжения, то она полагается равной ей и сила взаимодействия узлов определяется исходя из двух допущений: величина нормальной составляющей N и направление касательной составляющей T остаются неизменными. Тогда компоненты силы, возникающей в контакте двух узлов при их взаимном проскальзывании,
) (3.41)
Прикладывая вычисленные силы к узлу 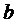и равные им по значению противоположного направления к узлу 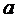,находим их перемщения 
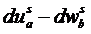, вызванные этими силами, используя уравнения (3.29).
Окончательно получаем перемещения узлов для случая их взаимного скольжения
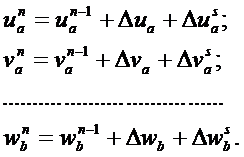(3.42)
В случае, если узлы на (n-1)-й прогонке находились в контакте и не теряют его на n-й прогонке, доля внедрения узла 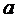полагается равной единице и решение выполняется по приведенному алгоритму с использованием зависимостей, начинвая с (3.31).
