Основные итерационные соотношения для трехмерной задачи
Для трехмерной задачи получение необходимых соотношений итерационного метода будет продемонстрировано на простейшем конечном элементе – тетраэдре с узлами в вершинах i,j,m,p .
Перемещения точек тетраэдра выражаются линейными законами:
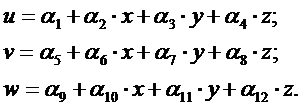(3.23)
Для определения коэффициентов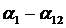 
в первое уравнение зависимостей (3.23) подставим координаты и перемещения четырех узлов тетраэдра. Полученная система из четырех уравнений позволяет найти коэффициенты
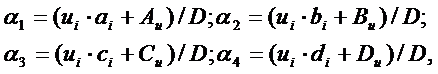(3.24)
где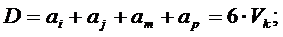 
- объем тетраэдра;
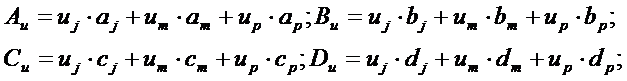
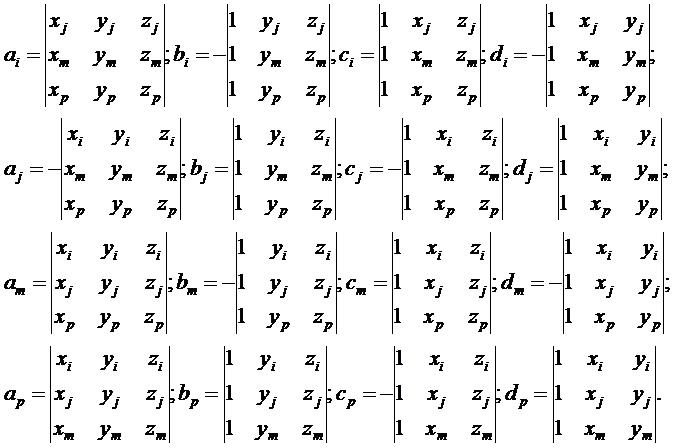
Аналогично получаются коэффициенты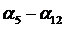 
с использованием второго и третьего уравнений зависимостей (3.23). В случае геометрически линейной задачи деформации определяют уравнениями Коши. Они постоянны по объему тетраэдра:
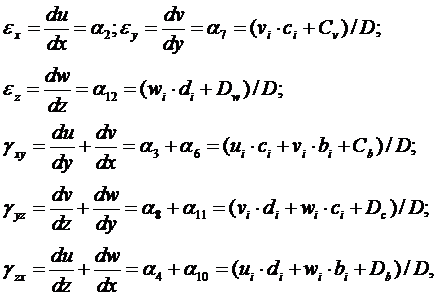(3.25)
где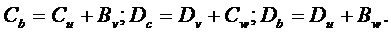 
Слагаемые с индексами перемещений имеют ту же структуру, что и (3.24) с заменой перемещений u на перемещения, соответствующие индексу.
Объемная деформация
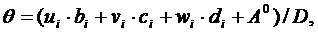
где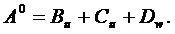 
Компоненты напряжения в конечном элементе
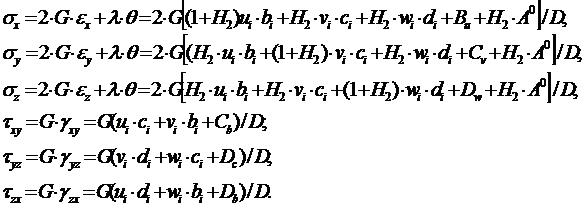(3.26)
Уравнения для определения перемещений узла при выполнении блочной итерации получим, используя принцип возможных перемещений,
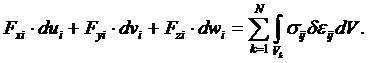(3.27)
Выразим вариации деформации через вариации перемещений
(3.28)
Взяв интегралы, стоящие в правой части уравнения (3.27) и приравняв коэффициенты при независимых вариациях перемещений равными нулю, получим систему из трех уравнений для определения перемещения узла i:
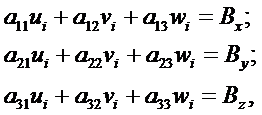(3.29)
(3.30)
где 
, 
, 
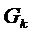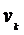- соответственно модуль упругости второго рода, коэффициент Пуассона материала конечного элемента и ушестеренный объем k-го тетраэдра.
