Физические и математические расчетные схемы амортизатора удара
Значительные исследования по определению характеристик фрикционных амортизаторов удара, влиянию их на особенности ударных нагрузок подвижного состава, по разработке их математических моделей проведены учёными БИТМа под руководством Л.Н. Никольского [47-50].
К настоящему времени разработаны математические модели, позволяющие с достаточной достоверностью и точностью оценивать влияние силовых характеристик поглощающих аппаратов автосцепки на уровень продольных сил и ускорений при режимах неустановившегося движения. При этом в зависимости от решаемой задачи им может быть придан как детерминированный, так и стохастический характер.
Свойства амортизатора могут быть описаны с различной степенью пол¬ноты математическими моделями различной степени сложности. Выбор той или иной математической модели амортизатора зависит от поставлен¬ной перед исследователем задачи и неразрывно связан с проблемой идентификации модели, нахождением способов определения сис¬темы входящих в нее параметров.
Рассмотрим различные модели процессов, протекающих в аморти¬заторе.
Все математические модели фрикционных аппаратов можно разделить на две принципиально различные группы в зависимости от того, учиты¬вают они или нет инерционные свойства силовой системы амортизатора. В большинстве случаев эти свойства игнорируются; силовая система, по терминологии теории автоматического регулирования, рассматривается как безынерционное усилительное звено, в котором связь между входом (силой сжатия пружин подпора Pпр) и выходом (силой сжатия аппарата P) устанавливается мгновенно с помощью соотношения.
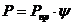 (1.1)
(1.1)
где 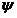 эффициент передачи.
эффициент передачи.
В формуле (1.1) 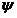 имеет смысл коэффициента усиления.
имеет смысл коэффициента усиления.
Для математических моделей этой группы вводится понятие «силовая характеристика» Р (х, v), которая дает возможность устанавливать одно¬значную связь силы сжатия аппарата со сжатием х и скоростью сжатия v.
Учет инерционных свойств силовой системы позволяет представить амортизатор в качестве инерционных или колебательных звеньев, для ко¬торых установление однозначного, не зависящего от времени соотношения невозможно, а понятие «силовая характеристика» не имеет смысла. Математические модели такого типа в ряде случаев оказываются весьма эффективными, способными объяснить и математически описать наблю¬даемые в практике исследований поглощающих аппаратов физические за¬кономерности.
Считаем, что связь между Р и х определяется условием равновесия сил при равномерном движении; все детали аппаратов, кроме полимерных блоков, предполагаются недеформируемыми.
Представление силовой системы фрикционного амортизатора удара в ви¬де усилительного безынерционного звена с коэффициентом усиления 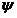 достаточно точна лишь для конструкций, обеспечива¬ющих монотонный характер изменения силы; в конструкциях, подвержен¬ных автоколебаниям, скорости и ускорения отдельных элементов сило¬вой системы изменяются очень быстро, инерционные силы в амортизато¬ре, несмотря на относительно малые массы деталей, оказываются соизме¬римыми с уровнем передаваемых амортизатором нагрузок. Это приводит к качественным и количественным изменениям в силовой характеристике аппарата.
достаточно точна лишь для конструкций, обеспечива¬ющих монотонный характер изменения силы; в конструкциях, подвержен¬ных автоколебаниям, скорости и ускорения отдельных элементов сило¬вой системы изменяются очень быстро, инерционные силы в амортизато¬ре, несмотря на относительно малые массы деталей, оказываются соизме¬римыми с уровнем передаваемых амортизатором нагрузок. Это приводит к качественным и количественным изменениям в силовой характеристике аппарата.
Рассмотрим более подробно силовую характеристику пластинчатого аппарата. Представленная в [48] мате¬матическая модель хорошо описывает работу аппарата при соу¬дарении одиночных вагонов и оказывается недостаточной для условий удара вагона в сцеп или условий работы вагона в поезде, когда возможен переход к этапу нагрузки после неполной разгрузки аппарата. Различный характер возможного изменения сил при подобных ситуа¬циях показан на рис. 1.6.
Введем, наряду с координатой х, определяющей перемещение детали 6 аппарата (рис. 1.5), координату z, устанавливающую положение его подвижных пластин. С ее помощью условия перехода с од¬ной ветви силовой характеристики на другую могут быть сформулирова¬ны следующим образом (коэффициенты передачи с индексом отвечают за разгрузку):
 (1.2)
(1.2)
где Pу (w,v) – упругая динамическая силовая характеристика подпорной части аппарата; w = x + x0, 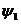 ,
, 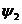 – коэффициенты передачи; i1 – коэффициент передачи при отсутствии трения. Коэффициенты передачи вычислялись по формулам (1.3 – 1.6).
– коэффициенты передачи; i1 – коэффициент передачи при отсутствии трения. Коэффициенты передачи вычислялись по формулам (1.3 – 1.6).
Рис. 1.6 Силовые характеристики пластинчатого аппарата при различных вариантах его нагружения
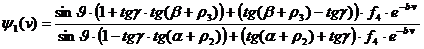 (1.3)
(1.3)
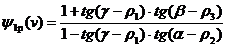 (1.4)
(1.4)
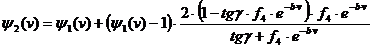 (1.5)
(1.5)
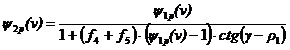 (1.6)
(1.6)
где 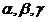 – параметры клиновой системы аппарата;
– параметры клиновой системы аппарата;
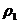 – угол трения на основных поверхностях;
– угол трения на основных поверхностях;
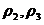 – углы трения на вспомогательных поверхностях;
– углы трения на вспомогательных поверхностях;
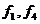 – коэффициенты трения на главных поверхностях;
– коэффициенты трения на главных поверхностях;
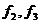 – коэффициенты трения на вспомогательных поверхностях;
– коэффициенты трения на вспомогательных поверхностях;
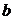 – коэффициент, учитывающий зависимость коэффициента трения от скорости скольжения.
– коэффициент, учитывающий зависимость коэффициента трения от скорости скольжения.
Углы трения представляют собой арктангенсы соответствующих коэффициентов трения, т.е. 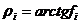
Коэффициент передачи при отсутствии трения вычисляется по формуле:
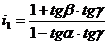 (1.7)
(1.7)
Превышение поглощающим аппаратом максимального хода, в уравнениях (1.2) учитывается введением дополнительного слагаемого, отвечающего за жесткость корпуса аппарата.
Приведенная математическая модель по сравнению с упрощенной моделью [47] вызывает необходимость вычисления и запомина¬ния на каждом шаге новой вспомогательной переменной z. Общим недостатком силовых характеристик, приведенных в [47], является разрывный характер зависимости Р (х, v) при переходе от нагруз¬ки к разгрузке и наоборот. Неопределенность силовой характеристики аппарата при v = 0 оказывает незначительное влияние на результаты моде¬лирования удара вагона в недеформируемый упор или в сцеп из несколь¬ких вагонов. Однако, как показывает практика расчетов на ЭВМ, эта не¬определенность способна приводить к значительным погрешностям при квазистатическом действии малоизменяющихся сил, характерном для мно¬гих режимов движения поездов.
Разрывный характер зависимости силы трения от скорости или пере¬мещения является результатом математической абстракции. В приведен¬ных выше формулах разрыв в зависимости силы трения от перемещения можно устранить, если учесть связь силы трения покоя со сдвиговой по¬датливостью контактной зоны деталей.
В данной работе предпринимается попытка построить модель аппарата в целом, опираясь на данные, полученные при статических испытаниях упругого комплекта и откорректированные после динамических экспериментов.