Метод «релаксации»
Итерационные зависимости для определения перемещений
Раскрытие статической неопределимости методом сил связано с трудностями при выборе основной системы и определении сил в стержнях, как от внешних нагрузок, так и от единичных неизвестных сил. Более удобно для конечно-элементной схемы получить решение в виде значений перемещений ее узлов. Такая информация позволяет наиболее просто получить деформации и напряжения в точках сплошной среды. Широкое применение для таких задач нашел метод перемещений, предполагающий наложение связей на все узлы расчетной схемы и выбор в качестве неизвестных перемещений узлов.
Система уравнений метода перемещений для определения неизвестных может быть представлена в виде
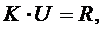(3.16)
где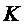 
-матрица жесткости; 
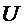- вектор узловых перемещений; 
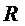- вектор узловых сил.
Для решения системы (3.16)чаще всего используют прямые методы: метод Гаусса, LDL-факторизация, разложение Холецкого, фронтальный и др. Из итерационных нашли применение методы Гаусса-Зейделя, метод последовательной верхней релаксации, градиентные методы групповой и блочной итерации. При применении итерационных методов на каждом шаге получается очередное приближение вектора перемещений узлов. При решении задач итерационными методами отмечена малая скорость сходимости, особенно на завершающем этапе. Но этот недостаток в какой-то мере может быть устранен применением блочной процедуры.
Необходимо отметить одно важное преимущество итерационного метода. Он позволяет в единой итерационной процедуре учесть геометрическую и физическую нелинейности, а также открывает хорошие перспективы решения контактных задач благодаря тому, что появляется возможность следить за перемещением узлов при выполнении итераций, устанавливать момент вхождения в контакт узлов, лежащих на контактных поверхностях, и с учетом трения в контакте определять величины компонентов контактных тел.
Для решения задачи итерационным методом необходимы зависимости, позволяющие найти уточненное значение перемещений i-го узла на очередной итерации. При блочной итерации с объединением в блок перемещени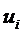й 
и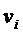 
узла i задача сводится к определению его перемещений в равновесное положение при освобождении его от связей и закрепленных в смещенных положениях окружающих узлах. Канонические уравнения метода итераций имеют вид
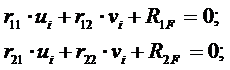(3.17)
где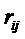 
- компоненты матрицы жесткости, по физическому смыслу представляющие собой силы, возникающие в i-й связи узла i при смещении его в направлении j-й связи на единицу; 
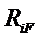- силы, возникающие в i-й связи от узловых сил 
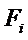и смещений соседних узлов.
Подстановка значений коэффициентов матрицы жесткости в систему уравнений (3.17) позволяет получить два уравнения для уточнения перемещений узла i на очередной итерации:
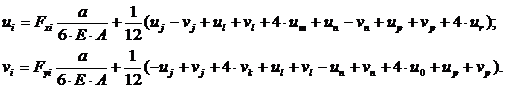(3.18)
Приписывая перемещениям узлов индексы, совпадающие с относительными координатами узла, зависимости (3.18) можно представить в более удобном для алгоритмизации виде:
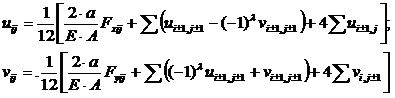(3.19)
