Составление и решение системы канонических уравнений
Рассмотрим методику получения уравнений метода сил, применительно к контактной задаче на плоскости. Допустим, что геометрические границы активного и пассивного тел, описываются точками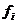 
и 
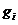соответственно (рис. 3.3).
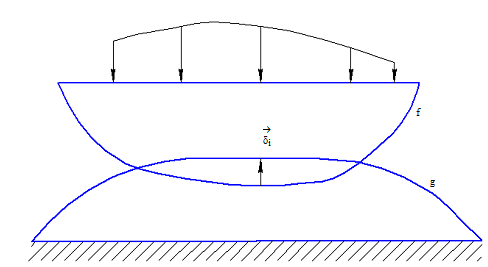
Рис. 3.3. К определению значения зазора
Вектора внутренних нормалей для узлов этих же тел обозначим, как 
и 
. Величина зазора определяется проекцией вектора 
(см. рис. 3.3) на направление внутренней нормали активного тела . Если из каких-либо соображений принять набор точек контакта, то величину зазора для каждой из таких точек можно записать как:
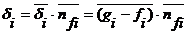(3.6)
При этом нужно учесть, что положение точек 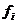и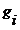 
складываются из их первоначального положения, смещения за счет движения тела как абсолютно твердого, а также за счет деформаций обусловленных действием контактных сил, неисключенных реакций и внешней нагрузки:
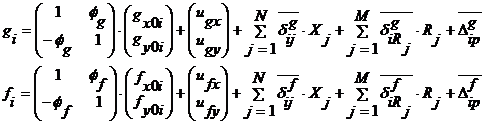(3.7)
где 
, 
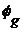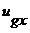и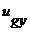 
- степени свободы пассивного тела;
, 
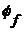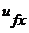и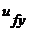 
- степени свободы активного тела;
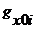и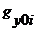 
- координаты точек пассивной поверхност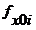и;
и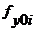 
- координаты точек активной поверхност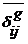и;
и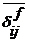 
- вектора перемещений i-тых точек пассивной и активной поверхностей от действия единичных сил приложенных в точках j-той пары контакта;
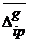и 
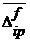- вектора перемещений i-тых точек пассивной и активной поверхностей от действия внешних сил;
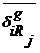и 
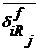- вектора перемещений i-тых точек пассивной и активной поверхностей от действия единичных сил приложенных в точках неисключенных реакций;
N – количество пар контакта, определяемое на основе принятого размера пятна контакта;
M – количество неисключенных реакций.
Подставляя выражения (3.7) в формулу (3.6), получим:
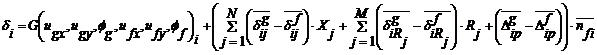(3.8)
где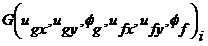 
- линейная функция относительно параметров смещения тел, входящих в систему, которая определяется из уравнения:
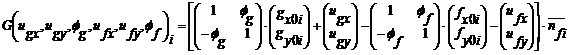(3.9)
Первое слагаемое в выражение (3.8) представляет собой составляющую зазора между активными и пассивными узлами поверхности, обусловленную начальными зазорами и перемещением тел, как абсолютно жестких те. Оставшиеся же слагаемые отвечают за деформационные перемещения узлов. После простых преобразований выражения (3.8) можно получить:
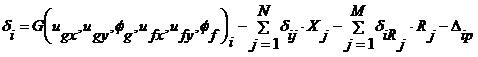(3.10)
где
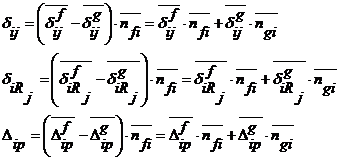(3.11)
Поскольку мы составляем уравнения зазора для i-той пары контакта, т.е. для точек на активном и пассивном телах, которые должны совпасть на общей поверхности контакта, то можно записать следующее уравнение, выражающее уравнения канонической системы метода сил:
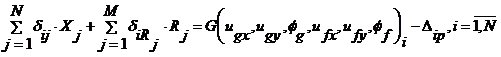(3.12)
Оставшиеся М уравнений метода сил для неисключенных реакций необходимо составить по аналогии с уравнениями для контактных сил. Единственным принципиальным отличием будет то, что величина зазора, определяемая геометрией и смещением тела, как абсолютно твердого, будет нулевой. Это и понятно, ведь точка, на которую наложена связь, остается неподвижной. Поэтому по аналогии с уравнением (3.12) запишем:
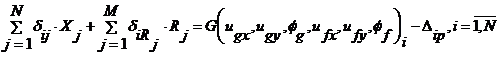(3.13)
где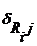 
- перемещение точки, в которой приложена неисключенная реакция в направлении исключенной связи от действия j-той единичной силы;
- перемещение точки, в которой приложена неисключенная реакция в направлении исключенной связи от действия другой неисключенной реакции.
Особенно следует отметить, что полученная система уравнений является параметризованной, поскольку в правой части системы уравнений (3.12) стоят линейные выражения относительно параметров смещения. Поэтому фактически для конкретного случая плоского контакта 2-х тел необходимо решить систему канонических уравнений для 7-ми правых частей. Эту задачу можно упростить, если не учитывать заведомо нулевые степени свободы. Впрочем, это детали реализации.
Подводя итог, можно сказать, что по результатам решения канонической системы уравнений метода сил мы получаем набор контактных сил и неисключенных реакций отброшенных связей в виде параметризованных линейных выражений, в которых параметрами выступают перемещения тел контакта, как абсолютно твердых тел:
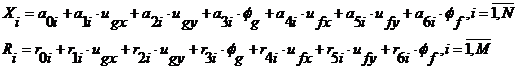(3.14)
